All Insights
Articles

Data should provide your questions, not just your answers
Articles
Diving into the deep blue data lake, maths in 3072 dimensions, and the perfect recipe for Data Spaghetti
Articles
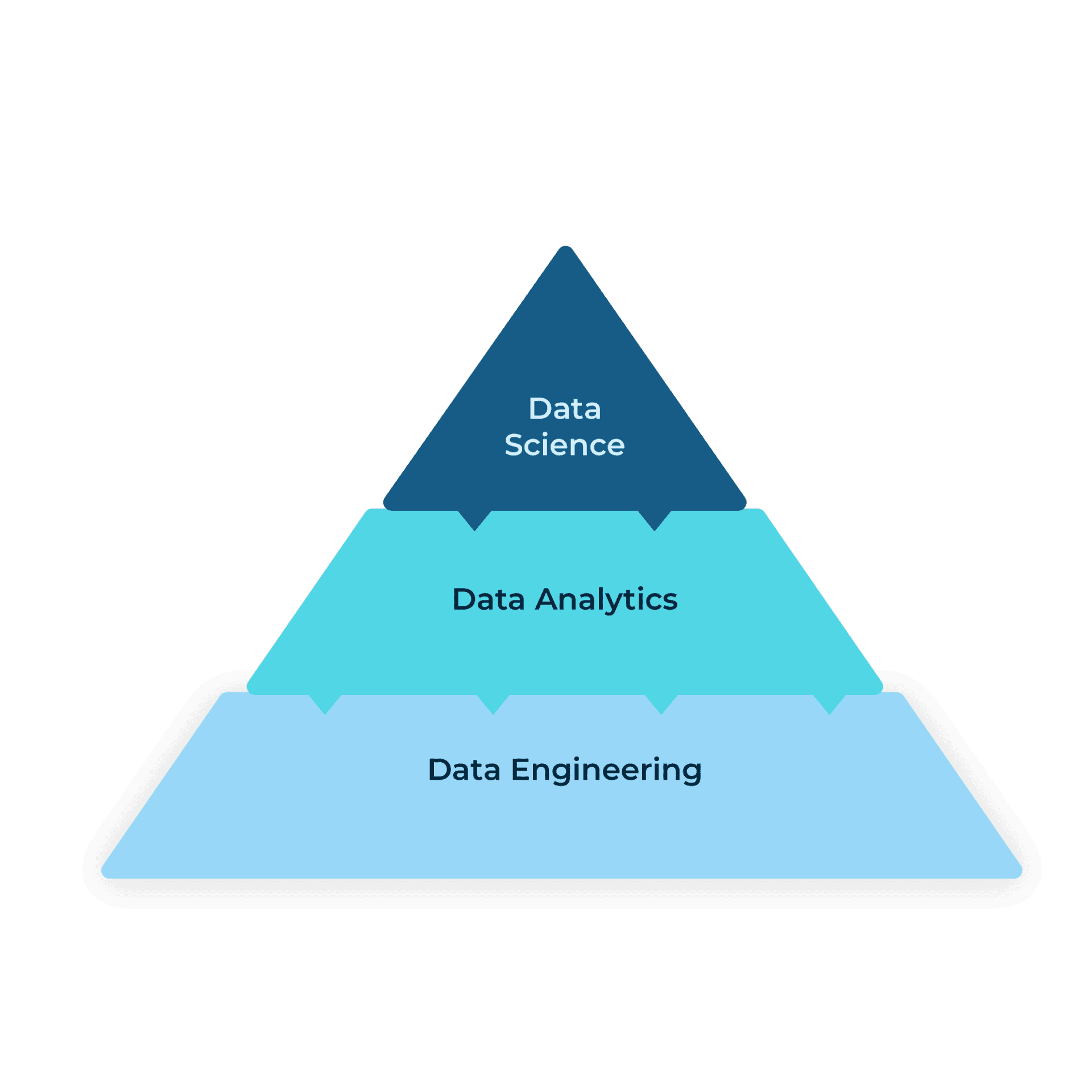
What’s up with all these “Data-X” words?
Podcasts

Data as an Asset: Navigating the Future with BDO’s Chief Data Officer, Denholm Hesse
Articles
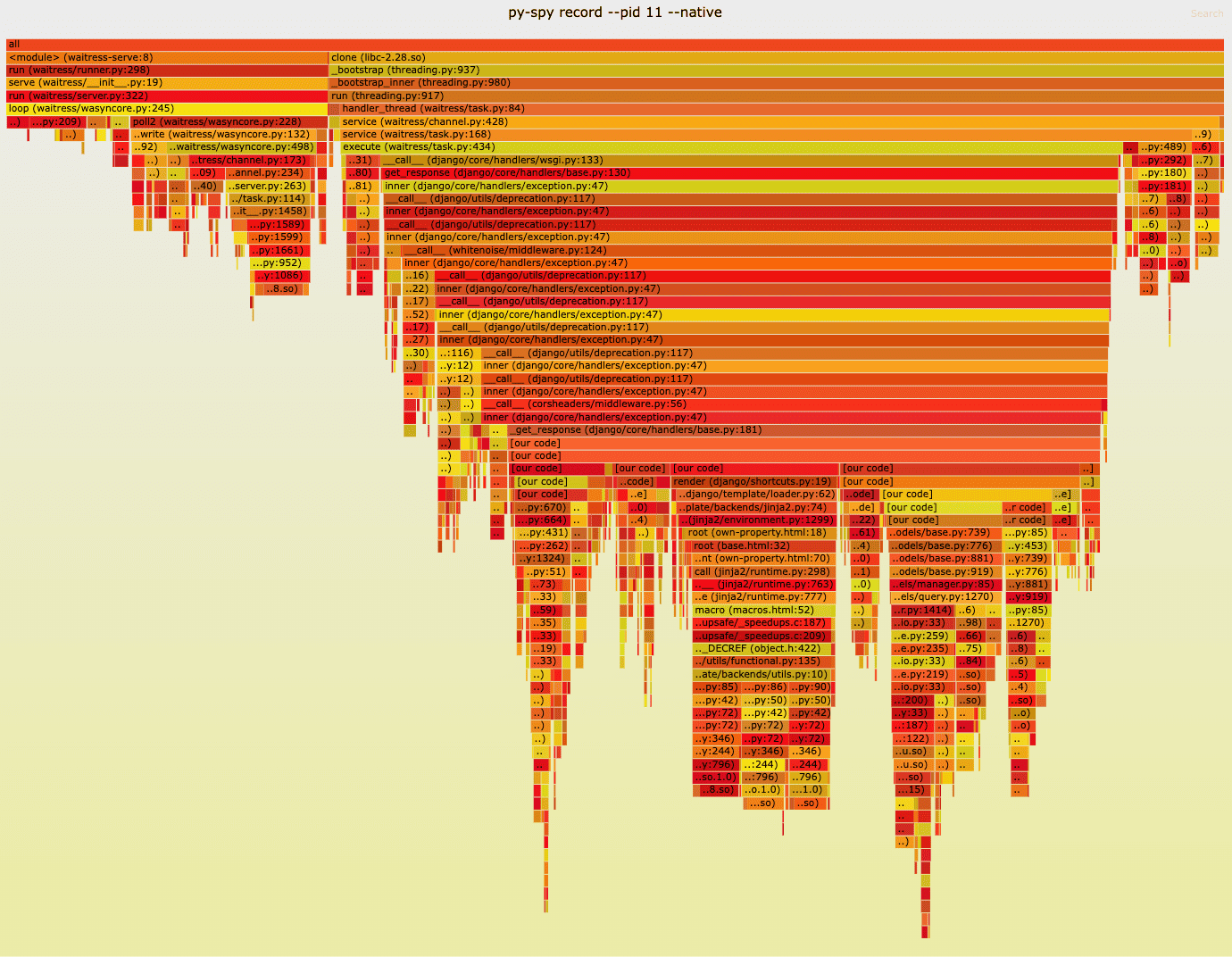
A love letter to flame graphs: or why the perfect visualisation makes the problem obvious
Articles

Showing up as a real human person is the only way to be an effective mentor and manager
Articles

Women in tech only want one thing and it’s…
Articles

Six senior Softwire women on careers, self-belief and success
Podcasts

Podcast: Empowering Innovation: Women Who Code with Rajani Rao
Podcasts

Podcast: Thomas Harris on navigating digital transformation: Insights from MasterCard’s journey
Podcasts

Podcast: Herb Kim – Why you need to risk failure to become a great leader
Podcasts

